Number of vibrational modes




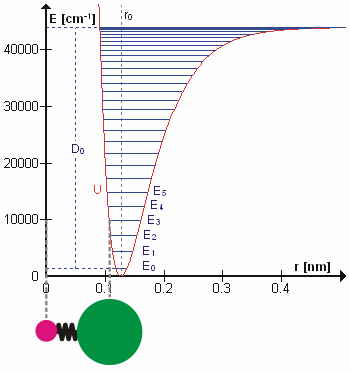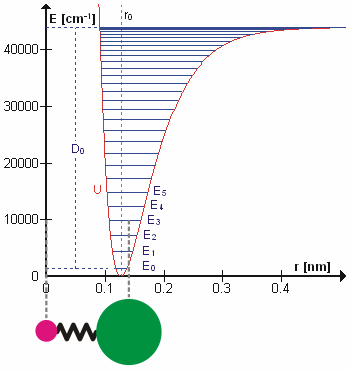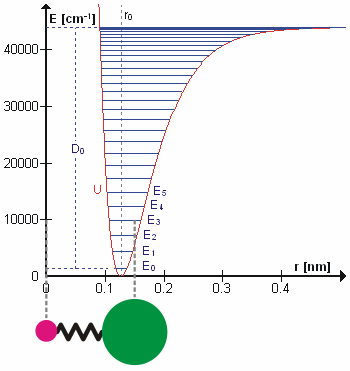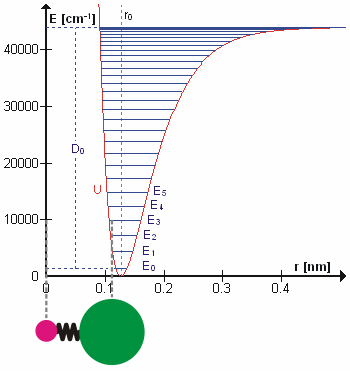
For a molecule with N atoms, the positions of all N nuclei depend on a total of 3N coordinates, so that the molecule has 3N degrees of freedom including translation, rotation and vibration. Translation corresponds to movement of the center of mass whose position can be described by 3 cartesian coordinates.

A nonlinear molecule can rotate about any of three mutually perpendicular axes and therefore has 3 rotational degrees of freedom. For a linear molecule, rotation about the molecular axis does not involve movement of any atomic nucleus, so there are only 2 rotational degrees of freedom which can vary the atomic coordinates.

An equivalent argument is that the rotation of a linear molecule changes the direction of the molecular axis in space, which can be described by 2 coordinates corresponding to latitude and longitude. For a nonlinear molecule, the direction of one axis is described by these two coordinates, and the orientation of the molecule about this axis provides a third rotational coordinate.

The number of vibrational modes is therefore 3N minus the number of translational and rotational degrees of freedom, or 3N–5 for linear and 3N–6 for nonlinear molecules.

Comments

Post a Comment

Popular posts from this blog

Molecular vibration

Image
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies , range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1. In general, a non-linear molecule with N atoms has 3 N – 6 normal modes of vibration, but a linear molecule has 3 N – 5 modes, because rotation about the molecular axis cannot be observed. A diatomic molecule has one normal mode of vibration, since it can only stretch or compress the single bond. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of different parts of the molecule. A molecular vibration is excited when the molecule absorbs energy, ΔE , corresponding to the vibration's frequency, ν , according to the relation ΔE = hν , where h is Planck
Read more

Vibrational coordinates

Image
The coordinate of a normal vibration is a combination of changes in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency ν , the frequency of the vibration. Internal coordinates edit Internal coordinates are of the following types, illustrated with reference to the planar molecule ethylene, Stretching: a change in the length of a bond, such as C–H or C–C Bending: a change in the angle between two bonds, such as the HCH angle in a methylene group Rocking: a change in angle between a group of atoms, such as a methylene group and the rest of the molecule. Wagging: a change in angle between the plane of a group of atoms, such as a methylene group and a plane through the rest of the molecule, Twisting: a change in the angle between the planes of two groups of atoms, such as a change in the angle between the two methylene groups. Out–of–plane: a change in the angle between any one of the C–H bonds and the plane defi
Read more