Vibrational coordinates

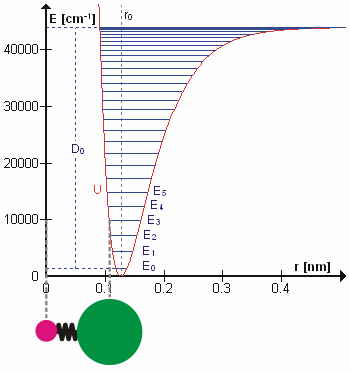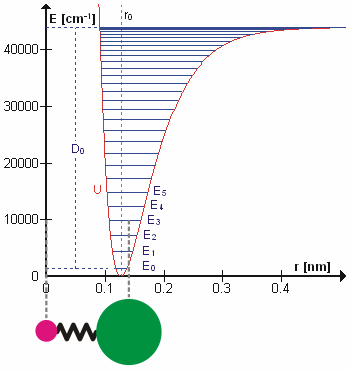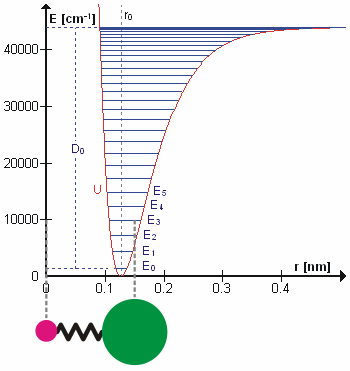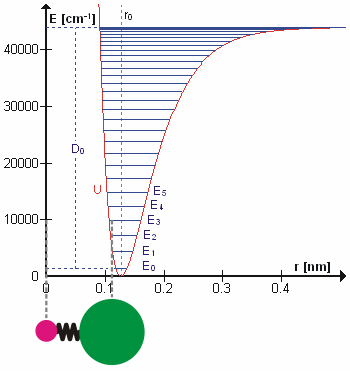
The coordinate of a normal vibration is a combination of changes in the positions of atoms in the molecule. When the vibration is excited the coordinate changes sinusoidally with a frequency ν, the frequency of the vibration.

Internal coordinatesedit

Internal coordinates are of the following types, illustrated with reference to the planar molecule ethylene,

• Stretching: a change in the length of a bond, such as C–H or C–C
• Bending: a change in the angle between two bonds, such as the HCH angle in a methylene group
• Rocking: a change in angle between a group of atoms, such as a methylene group and the rest of the molecule.
• Wagging: a change in angle between the plane of a group of atoms, such as a methylene group and a plane through the rest of the molecule,
• Twisting: a change in the angle between the planes of two groups of atoms, such as a change in the angle between the two methylene groups.
• Out–of–plane: a change in the angle between any one of the C–H bonds and the plane defined by the remaining atoms of the ethylene molecule. Another example is in BF₃ when the boron atom moves in and out of the plane of the three fluorine atoms.

In a rocking, wagging or twisting coordinate the bond lengths within the groups involved do not change. The angles do. Rocking is distinguished from wagging by the fact that the atoms in the group stay in the same plane.

In ethene there are 12 internal coordinates: 4 C–H stretching, 1 C–C stretching, 2 H–C–H bending, 2 CH₂ rocking, 2 CH₂ wagging, 1 twisting. Note that the H–C–C angles cannot be used as internal coordinates as the angles at each carbon atom cannot all increase at the same time.

Vibrations of a methylene group (–CH₂–) in a molecule for illustrationedit

The atoms in a CH₂ group, commonly found in organic compounds, can vibrate in six different ways: symmetric and asymmetric stretching, scissoring, rocking, wagging and twisting as shown here:

Symmetrical stretching	Asymmetrical stretching	Scissoring (Bending)
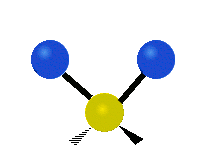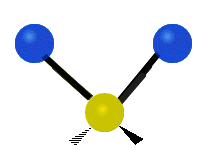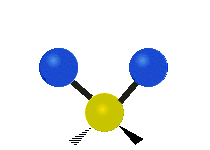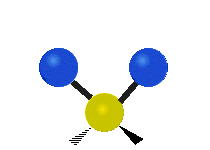
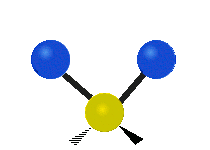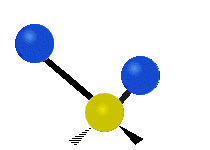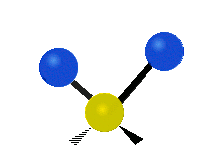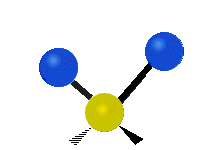
Rocking	Wagging	Twisting

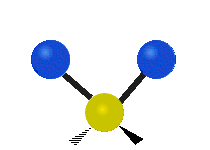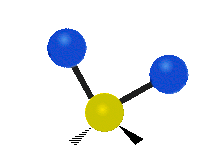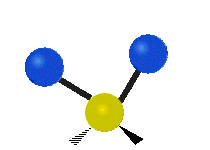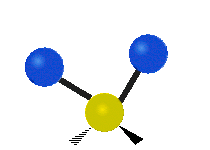
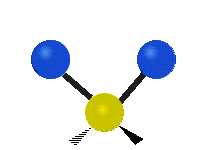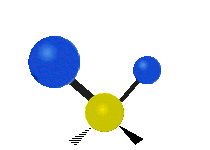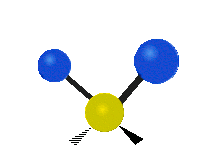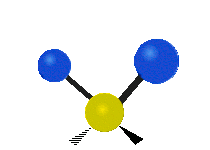
(These figures do not represent the "recoil" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms).

Symmetry–adapted coordinatesedit

Symmetry–adapted coordinates may be created by applying a projection operator to a set of internal coordinates. The projection operator is constructed with the aid of the character table of the molecular point group. For example, the four (un–normalized) C–H stretching coordinates of the molecule ethene are given by

${\displaystyle Q_{s1}=q_1+q_2+q_3+q_4}$

${\displaystyle Q_{s2}=q_1+q_2-<!--\; -\; -->q_3-<!--\; -\; -->q_4}$

${\displaystyle Q_{s3}=q_1-<!--\; -\; -->q_2+q_3-<!--\; -\; -->q_4}$

${\displaystyle Q_{s4}=q_1-<!--\; -\; -->q_2-<!--\; -\; -->q_3+q_4}$

where ${\displaystyle q_1-<!--\; -\; -->q_4}$ are the internal coordinates for stretching of each of the four C–H bonds.

Illustrations of symmetry–adapted coordinates for most small molecules can be found in Nakamoto.

Normal coordinatesedit

The normal coordinates, denoted as Q, refer to the positions of atoms away from their equilibrium positions, with respect to a normal mode of vibration. Each normal mode is assigned a single normal coordinate, and so the normal coordinate refers to the "progress" along that normal mode at any given time. Formally, normal modes are determined by solving a secular determinant, and then the normal coordinates (over the normal modes) can be expressed as a summation over the cartesian coordinates (over the atom positions). The normal modes diagonalize the matrix governing the molecular vibrations, so that each normal mode is an independent molecular vibration. If the molecule possesses symmetries, the normal modes "transform as" an irreducible representation under its point group. The normal modes are determined by applying group theory, and projecting the irreducible representation onto the cartesian coordinates. For example, when this treatment is applied to CO₂, it is found that the C=O stretches are not independent, but rather there is an O=C=O symmetric stretch and an O=C=O asymmetric stretch:

• symmetric stretching: the sum of the two C–O stretching coordinates; the two C–O bond lengths change by the same amount and the carbon atom is stationary. Q = q₁ + q₂
• asymmetric stretching: the difference of the two C–O stretching coordinates; one C–O bond length increases while the other decreases. Q = q₁ - q₂

When two or more normal coordinates belong to the same irreducible representation of the molecular point group (colloquially, have the same symmetry) there is "mixing" and the coefficients of the combination cannot be determined a priori. For example, in the linear molecule hydrogen cyanide, HCN, The two stretching vibrations are

• principally C–H stretching with a little C–N stretching; Q₁ = q₁ + a q₂ (a << 1)
• principally C–N stretching with a little C–H stretching; Q₂ = b q₁ + q₂ (b << 1)

The coefficients a and b are found by performing a full normal coordinate analysis by means of the Wilson GF method.